Mathematical expressions
Introduction
LaTeX's features for typesetting mathematics make it a compelling choice for writing technical documents. This article shows the most basic commands needed to get started with writing maths using LaTeX.
Writing basic equations in LaTeX is straightforward, for example:
\documentclass{article}
\begin{document}
The well known Pythagorean theorem \(x^2 + y^2 = z^2\) was
proved to be invalid for other exponents.
Meaning the next equation has no integer solutions:
\[ x^n + y^n = z^n \]
\end{document}
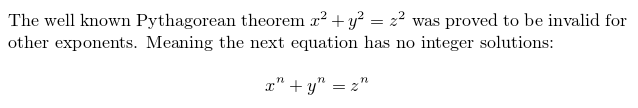
As you see, the way the equations are displayed depends on the delimiter, in this case \[...\] and \(...\).
Mathematical modes
LaTeX allows two writing modes for mathematical expressions: the inline math mode and display math mode:
- inline math mode is used to write formulas that are part of a paragraph
- display math mode is used to write expressions that are not part of a paragraph, and are therefore put on separate lines
Inline math mode
You can use any of these "delimiters" to typeset your math in inline mode:
\(...\)$...$\begin{math}...\end{math}
They all work and the choice is a matter of taste, so let's see some examples.
\documentclass{article}
\begin{document}
\noindent Standard \LaTeX{} practice is to write inline math by enclosing it between \verb|\(...\)|:
\begin{quote}
In physics, the mass-energy equivalence is stated
by the equation \(E=mc^2\), discovered in 1905 by Albert Einstein.
\end{quote}
\noindent Instead if writing (enclosing) inline math between \verb|\(...\)| you can use \texttt{\$...\$} to achieve the same result:
\begin{quote}
In physics, the mass-energy equivalence is stated
by the equation $E=mc^2$, discovered in 1905 by Albert Einstein.
\end{quote}
\noindent Or, you can use \verb|\begin{math}...\end{math}|:
\begin{quote}
In physics, the mass-energy equivalence is stated
by the equation \begin{math}E=mc^2\end{math}, discovered in 1905 by Albert Einstein.
\end{quote}
\end{document}
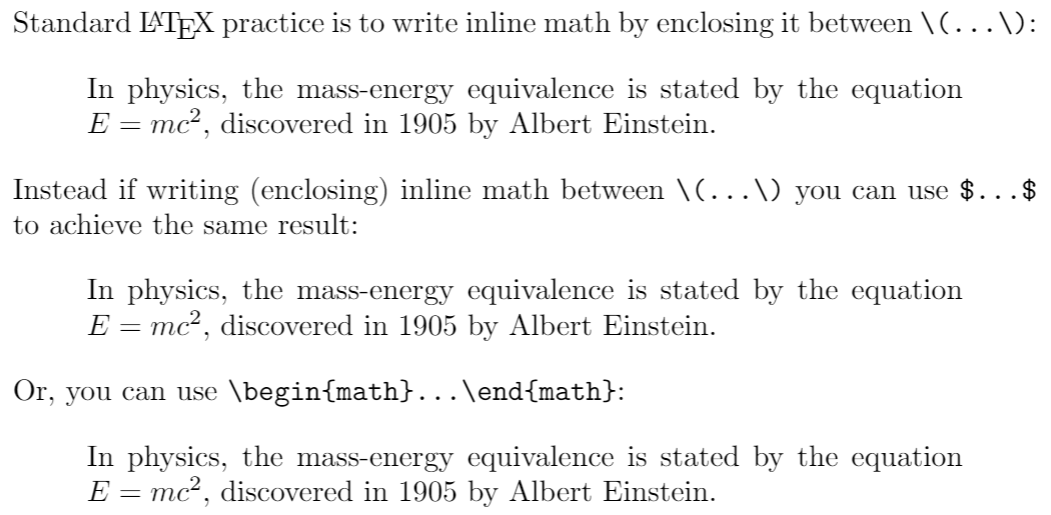
Display math mode
Use one of these constructions to typeset maths in display mode:
\[...\]\begin{displaymath}...\end{displaymath}\begin{equation}...\end{equation}
Display math mode has two versions which produce numbered or unnumbered equations. Let's look at a basic example:
\documentclass{article}
\begin{document}
The mass-energy equivalence is described by the famous equation
\[E=mc^2\]
discovered in 1905 by Albert Einstein.
In natural units ($c$ = 1), the formula expresses the identity
\begin{equation}
E=m
\end{equation}
\end{document}
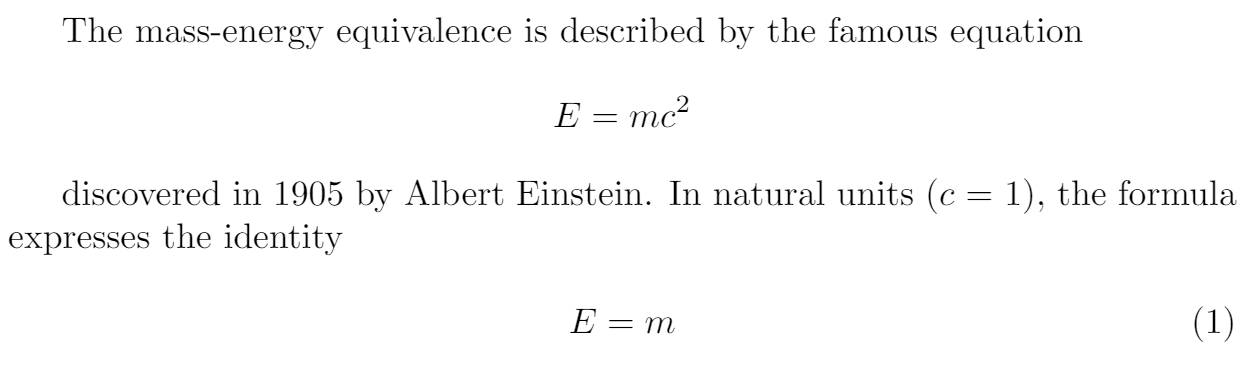
Another example
The following example uses the equation* environment which is provided by the amsmath package—see the amsmath article for more information.
\documentclass{article}
\usepackage{amsmath} % for the equation* environment
\begin{document}
This is a simple math expression \(\sqrt{x^2+1}\) inside text.
And this is also the same:
\begin{math}
\sqrt{x^2+1}
\end{math}
but by using another command.
This is a simple math expression without numbering
\[\sqrt{x^2+1}\]
separated from text.
This is also the same:
\begin{displaymath}
\sqrt{x^2+1}
\end{displaymath}
\ldots and this:
\begin{equation*}
\sqrt{x^2+1}
\end{equation*}
\end{document}

Reference guide
Below is a table with some common maths symbols. For a more complete list see the List of Greek letters and math symbols:
| description | code | examples |
|---|---|---|
| Greek letters | \alpha \beta \gamma \rho \sigma \delta \epsilon |
$$ \alpha \ \beta \ \gamma \ \rho \ \sigma \ \delta \ \epsilon $$ |
| Binary operators | \times \otimes \oplus \cup \cap |
|
| Relation operators | < > \subset \supset \subseteq \supseteq |
|
| Others | \int \oint \sum \prod |
Different classes of mathematical symbols are characterized by different formatting (for example, variables are italicized, but operators are not) and different spacing.
Further reading
The mathematics mode in LaTeX is very flexible and powerful, there is much more that can be done with it:
Overleaf guides
- Creating a document in Overleaf
- Uploading a project
- Copying a project
- Creating a project from a template
- Using the Overleaf project menu
- Including images in Overleaf
- Exporting your work from Overleaf
- Working offline in Overleaf
- Using Track Changes in Overleaf
- Using bibliographies in Overleaf
- Sharing your work with others
- Using the History feature
- Debugging Compilation timeout errors
- How-to guides
- Guide to Overleaf’s premium features
LaTeX Basics
- Creating your first LaTeX document
- Choosing a LaTeX Compiler
- Paragraphs and new lines
- Bold, italics and underlining
- Lists
- Errors
Mathematics
- Mathematical expressions
- Subscripts and superscripts
- Brackets and Parentheses
- Matrices
- Fractions and Binomials
- Aligning equations
- Operators
- Spacing in math mode
- Integrals, sums and limits
- Display style in math mode
- List of Greek letters and math symbols
- Mathematical fonts
- Using the Symbol Palette in Overleaf
Figures and tables
- Inserting Images
- Tables
- Positioning Images and Tables
- Lists of Tables and Figures
- Drawing Diagrams Directly in LaTeX
- TikZ package
References and Citations
- Bibliography management with bibtex
- Bibliography management with natbib
- Bibliography management with biblatex
- Bibtex bibliography styles
- Natbib bibliography styles
- Natbib citation styles
- Biblatex bibliography styles
- Biblatex citation styles
Languages
- Multilingual typesetting on Overleaf using polyglossia and fontspec
- Multilingual typesetting on Overleaf using babel and fontspec
- International language support
- Quotations and quotation marks
- Arabic
- Chinese
- French
- German
- Greek
- Italian
- Japanese
- Korean
- Portuguese
- Russian
- Spanish
Document structure
- Sections and chapters
- Table of contents
- Cross referencing sections, equations and floats
- Indices
- Glossaries
- Nomenclatures
- Management in a large project
- Multi-file LaTeX projects
- Hyperlinks
Formatting
- Lengths in LaTeX
- Headers and footers
- Page numbering
- Paragraph formatting
- Line breaks and blank spaces
- Text alignment
- Page size and margins
- Single sided and double sided documents
- Multiple columns
- Counters
- Code listing
- Code Highlighting with minted
- Using colours in LaTeX
- Footnotes
- Margin notes
Fonts
Presentations
Commands
Field specific
- Theorems and proofs
- Chemistry formulae
- Feynman diagrams
- Molecular orbital diagrams
- Chess notation
- Knitting patterns
- CircuiTikz package
- Pgfplots package
- Typesetting exams in LaTeX
- Knitr
- Attribute Value Matrices
Class files
- Understanding packages and class files
- List of packages and class files
- Writing your own package
- Writing your own class






